结合专家判断与算法分析的软件迁移成本估算模型(估算项目模型方法迁移)

传统的软件成本估算方法往往基于历史数据、专家判断或简单的数学模型，但这些方法往往难以准确反映项目的实际情况。
因此，本文提出了一种混合方法，该方法结合了任务离散化、专家判断和现代算法技术，旨在提高软件项目工期估算的准确性和适应性。

通过引入基于容量和复杂性的双因素鉴定系统，我们构建了一个更为精细和全面的软件项目工期估算模型。
该模型特别关注大型遗留系统的迁移项目，充分考虑了系统复杂性、技术债务、资源瓶颈等因素，为项目团队提供了更加准确和实用的工期估算工具。

本文介绍了一种新颖的软件成本估算混合方法，该方法将软件离散化为更小的任务，并同时使用专家判断和算法技术。
通过使用基于容量和复杂性的双因素鉴定系统，我们提出了一种更具适应性和可扩展性的软件项目工期估算模型，尤其侧重于大型遗留迁移项目。

软件成本估算（Software Cost Estimation，SCE）是软件工程领域的一个系统化定量过程，涉及分析、预测和分配软件系统开发、维护和管理所需的财务、时间和资源投资。

这项重要工作使用不同的方法、模型和技术，为利益相关者提供成功执行软件项目所需的预期财务、时间和资源评估。

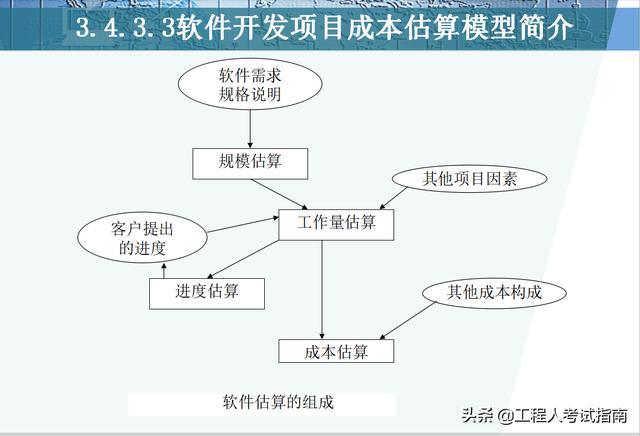
它是项目规划的重要组成部分，可以合理分配资源，支持软件开发生命周期中的风险评估和管理。

在软件工程领域，COCOMO（Constructive Cost Model，建构成本模型）模型是一个经过广泛验证的成本估算框架。
由 Barry Boehm 博士提出，COCOMO 深入探讨了软件属性与开发成本之间的复杂关系。

该模型具有层次化的结构，从基本到详细，提供了不同粒度的估算方法。
尽管模型主要基于代码行数和其他项目细节进行估算，但它也考虑了与经验成本数据的一致性。

随着软件开发范式的演变，COCOMO II 对模型进行了更新，以涵盖面向对象编程和敏捷开发方法论的复杂性。
尽管如此，过度依赖代码行数作为主要的估算标准仍是 COCOMO 面临的一个批评点，特别是在功能属性更为关键的项目中。

功能点分析法（Functional Point Analysis, FPA）是一个从软件功能角度出发的评估方法，它突破了传统的基于代码行数的估算模式。

该方法由 IBM 公司的 Allan Albrecht 在 20 世纪 70 年代末引入，强调以软件为用户提供的价值为基础，而非仅仅依赖于代码行数。
FPA 通过分类和评估不同的用户功能（如输入、输出、查询和界面），将软件复杂性转化为可量化的功能点。

这种方法特别适用于那些功能输出比底层代码更重要的项目。
FPA 以用户为中心，有效满足客户需求，并为开发团队和利益相关者提供了明确、可衡量的标准。
然而，其有效性高度依赖于对用户需求的深入理解，因此不确定性可能导致估算的偏差。

软件生命周期管理（Software Life Cycle Management，SLIM）是一个基于概率建模哲学的工具，由 Lawrence Putnam 设计。

该方法的本质是一组非线性方程，这些方程共同描绘了软件开发项目从启动到完成的轨迹。
SLIM 结合了历史数据和项目的具体情况，构建了一个概率景观，为项目团队提供了关于时间表、成本和潜在风险的有价值见解。

SLIM 的独特之处在于其动态性和适应性。
随着项目的推进，SLIM 能够根据反馈进行调整和重新配置，确保其估算始终与项目实际保持一致。
这种灵活性要求项目团队采取严谨的数据记录和跟踪方法。

总体而言，每种方法都有其独特的优点和适用场景。
在实际应用中，项目团队需要根据项目的具体需求和上下文来选择合适的估算方法。

在软件估算领域，专家判断（Expert Judgement）是一种古老而富有智慧的方法。
它摒弃了繁琐的算法，转而依赖资深行业专家积累的经验和直觉。

这些经验丰富的专家通过多年的项目实践，对项目的范围、复杂性和潜在挑战有着深刻的理解。
他们的直觉和洞察力能够弥补数据驱动模型的不足，捕捉到项目中难以量化的微妙之处。

然而，专家判断也有其局限性。
由于个人偏见和判断力的可变性，专家判断可能会受到主观因素的影响。
因此，在使用专家判断时，需要谨慎权衡其优点和潜在风险。

类比估算（Analogous Estimation），也称为历史数据估算（Historical Data Estimation），是一种利用历史项目数据为当前项目提供估算信息的方法。
这种方法通过回顾过去的项目，将类似项目的经验和成果应用于当前项目。

类比估算的有效性取决于历史数据的质量和相关性。
高质量、与当前项目相似的历史数据能够提供可靠的预测基础。
然而，如果历史数据与当前项目不匹配或过时，可能会导致估算的偏差。

因此，在使用类比估算时，需要仔细筛选和整理历史数据，确保其与当前项目具有足够的相似性。
同时，也要认识到类比估算的局限性，并在估算过程中保持谨慎和灵活性。

德尔菲技术（Delphi Technique）是一种集体预测方法，旨在通过收集专家小组的匿名见解和预测来达成共识。
该方法源自古代的德尔菲神谕，强调集体智慧和匿名性。

德尔菲技术通过多轮反馈和讨论，促进专家之间的交流和共识。
它有助于过滤掉异常值，趋向于更平衡的集体判断。
同时，匿名性有助于减少群体思维和影响性偏见的影响。

然而，德尔菲技术需要细致的引导和耐心。
它需要经过多轮审议和讨论才能达成共识，因此需要投入足够的时间和资源。
此外，由于德尔菲技术依赖于专家的参与，其效果也受到专家质量和参与度的影响。

总体而言，非算法方法如专家判断、类比估算和德尔菲技术在软件估算中发挥着重要作用。
它们提供了不同于数据驱动模型的视角和洞察力，有助于更全面地评估项目的复杂性和风险。
然而，这些方法也有其局限性，需要在实践中谨慎使用。

随着软件成本估算领域的不断发展，机器学习（ML）已经成为引领变革的重要力量。
与传统的确定性方法不同，机器学习深入概率领域，利用大量历史数据来发掘隐藏的模式和相关性。

通过在不同项目数据集上进行训练，ML 算法能够不断完善其预测能力，并适应那些传统、基于规则的系统经常忽略的细微差别。
在软件生态系统中，项目范围和挑战经常发生变化，这种动态性使得机器学习成为一种特别有效的工具。

然而，机器学习在 SCE 中的有效性高度依赖于训练数据的质量和全面性。
如果数据集稀少或存在偏差，可能会导致算法预测结果的不准确。
因此，强大的数据整理和验证机制在机器学习应用中至关重要。

神经网络（NN）是人工智能领域中的一个重要分支，其结构模仿了人类大脑神经元的复杂性。
通过采用节点和连接的分层架构，神经网络能够处理和解释各种信息。

在软件成本估算领域，神经网络能够从历史数据中识别和编织出复杂的模式，捕捉那些传统模型难以捉摸的非线性关系。
特别是随着多层架构的出现，神经网络的深度学习能力为 SCE 的复杂数据集提供了巨大的潜力。

然而，神经网络的深度学习能力也带来了透明度问题。
由于其“黑箱”性质以及可能出现的过度拟合现象，必须对神经网络进行细致的训练和验证，以确保估算结果的可靠性。
此外，最近的研究还表明，神经网络在训练过程中可能会经历所谓的“Grokking”阶段，这可能会为 SCE 领域带来新的发现和突破。

遗传算法（Genetic Algorithm，GA）是一种受自然进化启发的优化技术。
它将软件成本估算视为一个优化问题，通过模拟自然选择、交叉和变异等过程来寻找最佳的解决方案。

遗传算法从不同的估算策略群体开始，通过进化循环不断完善这些策略，从而逐渐逼近更优化的估算模型。
其固有的适应性和探索性使得遗传算法非常适合处理 SCE 中充满局部最优解的问题。

然而，由于遗传算法的随机性本质，其结果虽然在总体上是稳健的，但并不总是保证每次运行的绝对一致性。
为了平衡探索和利用之间的关系，对遗传算法的进化参数进行精细调整仍然至关重要。

敏捷方法（Agile Methodology）作为对传统软件开发流程的一种革新，为项目管理和产品交付方式带来了革命性的变革。
它强调迭代开发、跨职能团队协作以及持续的价值交付，这种理念同样延伸至敏捷估算技术中。

与传统的“一刀切”估算方式不同，敏捷估算技术更加注重随着项目进展和团队知识积累而进行的持续调整。
它强调的不是在项目初期就预测所有潜在复杂性，而是在整个项目生命周期中持续迭代和优化估算。

在敏捷估算中，团队通常使用故事点（而非小时或天数）来评估用户故事或工作项所需的相对工作量。
故事点综合考虑了任务的复杂性、潜在风险和工作量大小。

通过聚焦于相对工作量，团队能够避免由于未知挑战或依赖关系而导致的估算失真。
随着迭代的进行，团队会逐渐形成对“速度”（即每个迭代周期中完成的故事点平均数）的感性认知，从而更有效地预测未来的进度。

规划扑克牌是一种广泛应用的敏捷估算工具。
在规划会议中，团队成员（包括开发人员、测试人员和产品负责人）共同评估特定任务或用户故事的工作量。
每个成员从一套预设值（如斐波那契数列）的扑克牌中选择一张，以表示其估算结果。
在展示各自的扑克牌后，团队成员讨论差异，并通过协作讨论达成一致意见。

规划扑克牌的优势在于它能够将团队成员的个体知识整合为集体智慧，从而形成更为准确和可靠的估算结果。
同时，这一过程还有助于识别潜在的挑战和不确定性，进而做出更加明智的决策。

敏捷估算技术的核心在于其迭代性。
在项目的每个冲刺或迭代过程中，团队都会根据新的信息和实际经验对之前的估算进行调整。
这种持续的反馈循环确保了估算的准确性和预测的有效性随着项目的进展而不断提高。

我们的目标在于构建一个结合专家见解与算法精度的混合模型。
在考虑专家方法时，我们必须认识到，尽管它依赖于专业知识和经验，但也可能受到主观评价和个人偏好的影响，不同专家之间甚至可能出现意见分歧。

此外，专家方法可能受到专家认知偏差和近期经验过度依赖的影响，从而影响其准确性。

另一方面，算法方法虽然具有客观性，但在没有足够的专业知识指导下，可能难以正确应用，且可能过于关注某些不太相关的参数（如代码行数）。

因此，本文旨在开发一种新型的混合模型，该模型将独立于编程语言，并综合考虑项目、硬件和人员等多维因素，以提供更准确和全面的估算。

在软件工程领域，任务离散化（Task Discretization）已成为一种被广泛接受的方法。
该方法的核心思想是将大型软件项目分解为更小、更易于管理的任务单元。

通过识别软件组件（如屏幕、应用程序接口或 SQL 脚本）的离散性，任务离散化确保项目可以有序地分解为一致且可管理的模块。
这种方法的优势在于，它使得估算团队能够更清晰地理解他们正在评估的内容，同时避免了因元素差异而导致的调整需求。
在本文中，我们将这些元素称为“任务”。

离散化方法的优点在于，它提高了估算的准确性，同时增加了灵活性，允许团队根据项目的变化需求进行迭代调整。
此外，通过详细分析每个任务的特性，团队可以更有效地分配资源，并将技能精确地应用到最需要的地方。

然而，这种详细的任务分解方法也存在一些挑战。
特别是在大型项目中，过度的离散化可能导致管理上的复杂性增加，同时也有可能忽略某些看似次要但实际上关键的任务。
此外，过于关注细节有时可能会掩盖项目的整体目标，导致决策延迟，这被称为“分析瘫痪”。

因此，在采用任务离散化方法时，需要找到一个平衡点，既要确保估算的准确性和灵活性，又要避免过度离散化带来的管理挑战和决策延误。

在软件工程项目中，当任务被细化为具有同质属性时，确定如何分配适当的努力变得至关重要。
经过深入研究，我们识别出两个关键因素：复杂性（Complexity）和工作量（Volumetry），作为决定努力分配的通用指标。

复杂性反映了任务执行所需的技术敏锐度和难度。
例如，设计一个包含动态交互功能的用户界面可能被视为高复杂性任务。

工作量（或称为“规模”）则指的是任务所涉及的工作总量或元素数量。
例如，一个包含大量字段和交互元素的用户界面可能具有较大的工作量。

复杂性和工作量都采用 1 到 5 的整数评级，以便于量化和比较。
接下来，我们定义了一个努力值（E）的计算公式，以量化每个任务的相对努力需求：

E = C × V

其中，C 代表复杂性，V 代表工作量。
通过乘法运算，我们能够在高复杂性和高工作量之间建立直接联系，从而更准确地反映潜在的风险和成本。
由此公式得出的努力值可能包括以下整数：

[1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 20, 25]3.3、算盘系统（Abacus System）

在得到努力值之后，我们需要为每个值分配相应的工作天数。
这一步骤至关重要，通常需要经验丰富的架构师和技术专家参与。
为了确保估算的准确性和一致性，我们的模型只允许这些关键资源介入一次。

为了更精确地确定每个努力值对应的工作天数，我们建议使用算法来减少人为错误并提高估算的准确性。
这些算法可以基于三种不同的模型和两种起始标准来模拟和生成数据集：

我们考虑了三种数学模型来解释努力值与工作天数之间的关系：线性、二次和指数模型。
每种模型都反映了不同的增长模式：

这些模型可以根据实际项目需求进行调整，以确保估算的准确性和实用性。
最终，我们可以使用以下代码来模拟和生成这些模型的数据和图表：

# 清单1：日生成模型的Python代码import numpy as npimport matplotlib.pyplot as pltimport pandas as pd # Importing pandas for tabular display# Fixed effort valuesefforts = np.array([1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 20, 25])# ParametersMax_days = 25Step_Days = 0.25def linear_model(effort, max_effort, max_days, step_days): slope = (max_days - step_days) / max_effort return slope effort + step_days - slopedef quadratic_model(effort, max_effort, max_days, step_days): scale = (max_days - step_days) / (max_effort + 0.05 max_effort2) return scale (effort + 0.05 effort2)def exponential_model(effort, max_effort, max_days, step_days): adjusted_max_days = max_days - step_days + 1 base = np.exp(np.log(adjusted_max_days) / max_effort) return step_days + base effort - 1def logarithmic_model(effort, max_effort, max_days, step_days): scale = (max_days - step_days) / np.log(max_effort + 1) return scale np.log(effort + 1)# Rounding to nearest stepdef round_to_step(value, step): return round(value / step) steplinear_days = np.array([round_to_step(linear_model(e, efforts[-1], Max_days, Step_Days), Step_Days) for e in efforts])quadratic_days = np.array([round_to_step(quadratic_model(e, efforts[-1], Max_days, Step_Days), Step_Days) for e in efforts])exponential_days = np.array([round_to_step(exponential_model(e, efforts[-1], Max_days, Step_Days), Step_Days) for e in efforts])logarithmic_days = np.array([round_to_step(logarithmic_model(e, efforts[-1], Max_days, Step_Days), Step_Days) for e in efforts])# Plotplt.figure(figsize=(10,6))plt.plot(efforts, linear_days, label="Linear Model", marker='o')plt.plot(efforts, quadratic_days, label="Quadratic Model", marker='x')plt.plot(efforts, exponential_days, label="Exponential Model", marker='.')plt.plot(efforts, logarithmic_days, label="Logarithmic Model", marker='+')plt.xlabel("Effort")plt.ylabel("Days")plt.title("Effort to Days Estimation Models")plt.legend()plt.grid(True)plt.show()# Displaying data in table formatdf = pd.DataFrame({ 'Effort': efforts, 'Linear Model (Days)': linear_days, 'Quadratic Model (Days)': quadratic_days, 'Exponential Model (Days)': exponential_days, 'Logarithmic Model (Days)': logarithmic_days})display(df)仿真

以下是一个实际例子，展示了如何使用之前提到的参数（如步长天数和最大天数）来生成和可视化三种模型的结果。

图1：展示了三种模型在不同努力值下预测的工作天数数据。

图2：则是以图形方式展示了这三种模型的预测结果，帮助我们直观地比较不同模型之间的差异和特点。

通过这些图表，我们可以清晰地看到三种模型在“压缩”或“扩展”努力值与工作天数关系方面的差异，这将对估算的精确性、风险评估以及值之间的关联性产生不同的影响。

在深入探讨了我们的模型之后，接下来我们将通过一个具体的大型传统迁移项目案例来展示其实际应用价值。
此类项目通常面临着一系列独特的挑战，使得传统的估算方法难以适用。
正如我们在前文所述，这些挑战包括频繁的回归测试、过时技术的资源短缺、专业知识的集中、新功能集成的复杂性，以及性能问题等。
这些问题不仅增加了项目的成本，还可能加大风险。

迁移项目通常会受到成本的影响。
需要迁移的因素通常包括：

上述所有潜在原因都会增加成本和/或风险。
可能有必要考虑迁移有问题的技术构件。
实施主要取决于产生的成本，因此有必要进行准确估算。
不过，必须承认，在组织迁移过程中，技术变革必须伴随着人力和组织调整。

在这种情况下，我们的模型显得尤为适用。
它不仅能够量化工作量，还能够结合专家的判断来确保估算的准确性。
这种结合了算法和专家知识的方法，可以弥补传统方法在处理复杂迁移项目时的不足。

值得注意的是，技术迁移不仅仅是代码层面的转换，更涉及到人力和组织层面的调整。
在确定了目标架构和技术栈之后，团队可能会面临缺乏相关领域专家的问题。
这使得单纯依赖“专家判断”的方法变得不再可靠，而算法方法也可能因为缺乏足够的上下文信息而失效。

此外，传统的以代码行数为基础的估算方法，在这种场景下也显得过于简单和不准确。
因此，我们的模型通过综合考虑复杂性、工作量以及专家意见，提供了一个更加全面和精确的估算方案。

当然，这种估算主要聚焦于开发本身的工作量，而不包括规范阶段和相关的基础设施成本。
但即便如此，它仍然为项目团队提供了一个有力的工具，帮助他们更好地规划和管理资源，从而确保项目的顺利进行。

总的来说，我们的模型为大型传统迁移项目提供了一个有效的解决方案，它结合了算法和专家知识，确保了估算的准确性和实用性。
这对于那些面临着一系列独特挑战的传统迁移项目来说，无疑是一个巨大的福音。

在实施估算模型的过程中，我们将经历三个阶段：初始化、估算和最终确定。
下面，我将概述每个阶段的关键步骤和考虑因素。

在初始化阶段，首要任务是对要估算的技术组件进行解构。
这需要将复杂的系统拆分成一组组易于管理的统一任务。
以使用GWT前端调用AS400数据库的应用程序为例，可以将其拆分为前端和后端两个主要部分：

接下来，组建一个估算团队。
这个团队不一定需要具备目标技术的深厚背景，但应由熟悉现有项目的资源组成，最好是技术/功能组合，他们能够对每项任务的技术复杂性和工作量进行评估。

团队成立后，开始为解构后的主要组件列出详细的任务清单，确保每个任务都明确、可度量。

在估算阶段，团队将为每个任务分配复杂度和体积值。
这需要结合技术专家的意见和团队的共同判断，以确保评估的准确性和合理性。
同时，还需要设定与任务相关的工作天数基准值。

为了确定这些基准值，可以邀请目标技术领域的专家参与讨论和评审。
专家可以根据经验和对目标技术的了解，为团队提供有价值的反馈和建议。

完成这一步骤后，团队将得到一个基于天数/工作量的估算模型，以及一份带有相应工作量值的任务清单。

在最终确定阶段，团队将使用估算模型将努力值转换为实际的工作天数。
这一过程需要考虑多个因素，如任务之间的依赖关系、资源的分配和项目的整体进度等。

为了进行风险分析，可以使用以下标准：

基于这些标准，团队可以在风险较高的区域采取针对性的措施，如增加资源投入、调整任务优先级或寻求外部支持等，以确保项目的顺利进行。

通过这三个阶段的迭代和优化，混合模型能够为大型传统迁移项目提供准确的工作量估算和风险分析，帮助团队更好地规划和管理项目资源，确保项目的成功实施。

经过深入研究和实践应用，我们总结出了以下流程，这一流程是专家判断与算法分析相结合的混合形式化方法。

此方法特别契合迁移项目的实际需求，既充分利用了现有资源，又无需依赖高水平的专业知识，从而确保了项目的顺利进行。

图3：混合模型的完整流程

为了更直观地展示这一流程，我们还提供了另一种表示方法：

图4：混合模型的完整流程

这两种表示方法均清晰地展示了混合模型的核心步骤和关键环节，有助于项目团队更好地理解和应用该模型，从而确保迁移项目的成功实施。

综上所述，我们提出的模型为大型遗留系统迁移项目的成本估算提供了一种实用且灵活的方法论。

通过巧妙地结合专家判断与结构化算法分析，此模型克服了过时或复杂系统迁移过程中所面临的独特挑战。
它深刻认识到，准确衡量工作量和成本不仅涉及技术层面，还需考虑人力和组织转型的多个维度。

我们所采用的三阶段流程——初始化、估算和最终确定——确保了从项目分解到详细风险分析的全面而细致的评估。
这种混合模式特别适用于那些面临艰巨迁移任务的团队，为他们提供了制定明智决策和有效准备过渡的明确路径。

借助这种方法，企业能够驾驭复杂的迁移工作，确保更加平稳、高效地过渡到现代系统。

从上述讨论和研究结果来看，传统迁移项目所面临的独特挑战无法通过传统的软件成本估算方法得到妥善解决。
而我们提出的混合模型在启发式的专家判断方法与结构化的算法分析之间建立了桥梁，提供了一个平衡且适应性强的解决方案。
该模型的主要优势在于其高度的适应性和利用目标技术机构知识及特定专业知识的能力。

此外，该模型还能够将问题分解为一系列统一的任务，并以适当的粒度进行估算，从而确保了其在实际应用场景中的广泛适用性。
尽管混合模型的当前实施已经显示出其巨大的潜力，但未来的研究和改进仍有望进一步提高其实用性：

总之，混合模型在软件成本估算领域取得了显著的进步，特别是在处理遗留迁移项目方面。
然而，如同所有模型一样，它也是一个持续发展的过程。
通过不断的完善和改进，我们有望进一步提高其在实际应用中的适用性和有效性。

[1] Barry W. Boehm. Software engineering economics. IEEE Transactions on Software Engineering, SE-7(1):4–21, 1981.

[2] Barry W. Boehm, Chris Abts, A. Winsor Brown, Sunita Chulani, Bradford K. Clark, Ellis Horowitz, Ray Madachy, Donald J. Reifer, and Bert Steece. Cost models for future software life cycle processes: Cocomo 2.0. Annals of Software Engineering, 1(1):57–94, 2000.

[3] International Function Point Users Group (IFPUG). Function Point Counting Practices Manual. IFPUG, 2000. FPCPM.

[4] L.H. Putnam. A general empirical solution to the macro software sizing and estimating problem. IEEE Transactions on Software Engineering, 4:345–361, 1978.

[5] R.T. Hughes. Expert judgment as an estimating method. Information and Software Technology, 38(2):67–75, 1996.

[6] Christopher Rush and Rajkumar Roy. Expert judgment in cost estimating: Modelling the reasoning process. Unknown Journal Name.

[7] N. Dalkey. An experimental study of group opinion: the Delphi method. Futures, 1(5):408–426, 1969.

[8] Yibeltal Assefa, Fekerte Berhanu, Asnakech Tilahun, and Esubalew Alemneh. Software effort estimation using machine learning algorithm. In 2022 International Conference on Information and Communication Technology for Development for Africa (ICT4DA), pages 163–168, 2022.

[9] A. Venkatachalam. Software cost estimation using artificial neural networks. In Proc. Int. Conf. Neural Netw. (IJCNN-93-Nagoya Japan), volume 1, pages 987–990, Oct 1993.

[10] R. Poonam and S. Jain. Enhanced software effort estimation using multi-layered feed forward artificial neural network technique. Procedia Computer Science, 89:307–312, 2016.

[11] Alethea Power, Yuri Burda, Harri Edwards, et al. Grokking: Generalization beyond overfitting on small algorithmic datasets. arXiv preprint arXiv:2201.02177, 2022.

[12] B.K. Singh and A.K. Misra. Software effort estimation by genetic algorithm tuned parameters of modified constructive cost model for NASA software projects. International Journal of Computer Applications, 59:22–26, 2012.

[13] K. Hrvoje and S. Gotovac. Estimating software development effort using Bayesian networks. In 2015 23rd International Conference on Software, Telecommunications and Computer Networks, pages 229–233, Split, Croatia, September 16–18 2015.

[14] M. Cohn. Agile Estimating and Planning. Prentice Hall PTR, 2005.

[15] Saurabh Bilgaiyan, Santwana Sagnika, Samaresh Mishra, and Madhabananda Das. A systematic review on software cost estimation in agile software development. Journal of Engineering Science and Technology Review, 10(4):51–64, 2017.

[16] S. McConnell. Software Estimation: Demystifying the Black Art. Microsoft Press, 2006.

[17] C. Szyperski. Component Software: Beyond Object-Oriented Programming. Addison-Wesley, 2nd edition, 2002.

[18] N. E. Fenton and S. L. Pfleeger. Software Metrics: A Rigorous and Practical Approach. PWS Publishing Co., 1997.

[19] Harry M. Sneed and Chris Verhoef. Cost-driven software migration: An experience report. Software: Practice and Experience, 2020.