技术背景
1. 元件库的Symbol、2D封装,3D结构当前都是根据数据手册手工绘制,每个元件需要花费数小时绘制,每一家电子公司都需要花费大量人力处理;每年行业有数以万计的新元件诞生,迫切需要更为快捷的元器件库生成技术。
2. 传统的元件商城、第三方库提供商开发了自动生成技术,本质上还是规则驱动的自动化技术,泛化性和准确性差,后端需要大量的人工check和修改工作,迫切需要新技术加以改善。
3. 基于多模态预训练模型,能很好识别元件手册上的图文内容,与现有建库工具结合,有潜力按标准生成各种库模型。
技术挑战
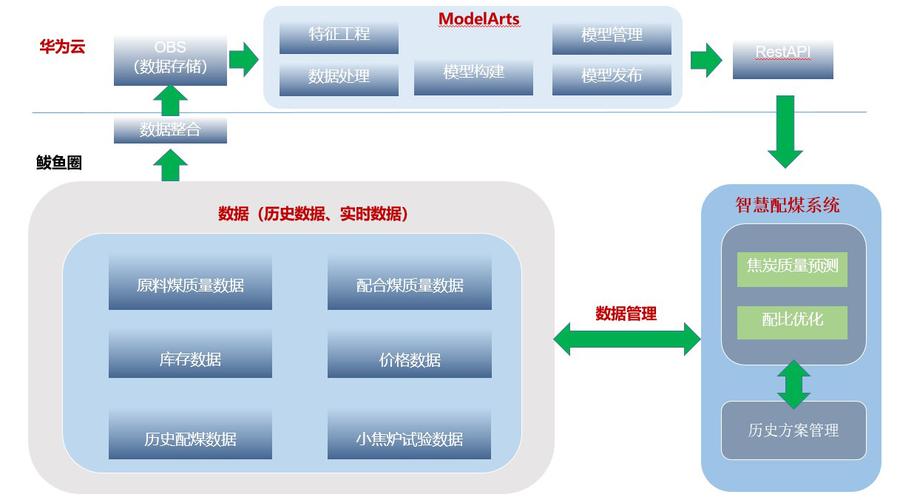
传统算法基于规则驱动的自动化设计技术,泛化性和准确性差,后端需要大量的人工check和修改工作。
多模态预训练模型有很好的语义理解、文本/表格/图形识别能力,可以很好解决泛化性问题,但对2D、3D物理图的高精度生成存在很大挑战。
技术诉求
技术需求:
提供基于多模态的专业电路设计预训练模型,输入元件Datasheet,输出该元件
Symbol符号库文件和封装图形库文件的生成,支持3D模型文件的生成。
技术指标:
1. 对于任意可解析、不加密、信息完整的Datasheet,Symbol符号库文件生成信息准确性大于99%;
2. 对于任意可解析、不加密、信息完整的Datasheet,封装图形库文件生成,图形精度0.01mm,识别信息描述准确性大于99%;
3. 对于任意可解析、不加密、信息完整的Datasheet, 3D模型文件生成,图形精度0.01mm。
集成需求:
集成华为云pEDA工具链EDM产品
约束条件:
使用预训练模型开发
参考文献
[1] S. Mori, Historical review of OCR research and development, 1992
[2] Tarek Ahmed Ibrahim Abdelaziz, Applications of integration of AI-based Optical Character
Recognition (OCR) and Generative AI in Document Understanding and Processing, 2023
[3] Fanghao Tian, Automatic Data Extraction Based on Semiconductor Datasheet for Design
Automation of Power Converters, 2022
链接:http://www.pi-lab.ac.cn/xsjl/faq/202401/t20240103_202005.html
难题二:基于结构刚度矩阵的迭代法预处理AI优化融合技术
技术背景
1. 结构大型稀疏刚度矩阵求解,尤其是结构自由度超过600W以上,直接法存在舍入误差、内存和硬盘开销过大及计算时间过长等致命缺点,迭代法的研制和开发成为另外一个重要选择。
2. 对于迭代法,迭代矩阵的选取具有决定作用。只有选取的迭代矩阵谱半径小于1才能保持迭代法收敛。在迭代矩阵谱半径小于1的情况下,值越小收敛速度越快。为加速求解原线性方程组的收敛速度问题,常用方法是对系数矩阵进行预处理,基于不同的迭代法,有不同的预处理技术,包括:小带宽部分处理、分解、分裂、多项式构造、重排序、子结构、区域分裂、多重网格等。
3. 不同的结构特点、网格和有限元模型建模方式不同,所产生方程组的系数矩阵的特性差异较大,目前无法使用一种通用的方法或理论进行预处理 而只能根据各自矩阵的特性采取适当的预处理方法,包括相应的设置参数。
4. 对各自工业实际场景产生的不同的系数矩阵和迭代法选择、预处理方法选择、最优参数构建机器学习或强化算法和策略、通过优化损失函数进行组合训练,通过评估后,提供用户基于各自矩阵特性,较优的自动化适配选择预处理方法和参数,保障迭代求解器的稳健性、稳定性和减少迭代时间。
5. 可行性分析:结构系数刚度矩阵的来源能够得到保障;迭代法和预处理已有成果基础;GNN图神经网格算法的成熟和不断应用,也非常适合稀疏矩阵特点;国产数值计算引擎+ 机器学习能力+麒麟欧拉的性能;国内CAE厂商对结构求解器的理解、结构仿真经验和工程场景基础;MIT CSAIL、Tsinghua University、Shanghai Qi Zhi Institute发表过Learning Preconditioners for Conjugate Gradient PDE Solvers,已经开展了不错工作,达成了较好效果
技术挑战
1. 结构系数刚度矩阵的特征描述和指标、分类和归类;
2. 结构系数刚度矩阵较多输入来源;
3. CG迭代法不同的预处理方法、预处理参数梳理和研制;
4. AI技术路线的选择,合适算法及学习路线;
5. 使用的校核、验证和优化技术
技术路线和达成指标
1. 结构系数刚度矩阵的特征描述和指标、分类和归类,保障 结构系数 刚度矩阵的数据输入;
2. 结构系数刚度矩阵输入、种类、指标参数:CG迭代法不同预处理方法、预处理参数的个数;
3. 机器学习或强化学习技术路线、算法和策略的选择;
4. 使用的损失函数优化、校核、验证和评估技术实现;
5. 可编译、运行适配麒麟处理器和欧拉系统;
6. 相比主流商软的预处理迭代法,在100个各类系数矩阵输入情况下,通过串行、SMP和DMP,达成计算精度相当,迭代步数和总体时间减少20%,稳健性、稳定性保障提升20%;
7. 虽然直接法具有稳定、通用和精度高,但内存开销高,数千万规模矩阵,直接法需数百G内存,如果AI优化融合的预处理矩阵合理,谱半径远小于1,迭代法仍然有求解速度高、精度能够满足数值计算精度要求的优势。
参考文献
链接:http://www.pi-lab.ac.cn/xsjl/faq/202401/t20240103_202007.html
难题三:刚柔耦合动力学系统实时仿真技术
技术背景
1、业务场景:
动力学系统的实时仿真性能是自动驾驶、数字孪生等领域的基本技术;其布置场景传统上需要模型简化后集成进入嵌入式系统,未来趋势是基于云平台用大规模物理模型直接开展实时仿真。解决方案是采用可大规模并行求解微分代数方程组的显式积分器,针对大规模物理模型用大步长并行的方法达到实时的目标;核心技术是对大型刚柔耦合系统进行物理建模,在保证计算精度的同时尽可能降低方程组的刚性,保证大步长计算过程的稳定性。
2、课题价值:
将实时仿真的实现从case by case层面提升到通用软件层面上进行实现,使其得到更广泛和更全面深入的应用,为自动驾驶,数字孪生等场景提供通用支持,进而创造更高的社会价值。
技术诉求
技术要求1:
以避免精度损失为前提,通过建模技术减小刚柔耦合多体模型的刚性以适用显式积分器求解,能够在给定的时间步长下保持稳定。
技术指标:
(1)刚性要求:中等刚性:系统的最大特征值/最小特征值不大于10000
(2)精度要求:位置与速度的计算结果与原系统模型的计算误差小于5%
(3)能量要求:保守系统采用显式积分器相较于隐式积分器,系统能量的守恒验证误差小于2%
技术要求2:
构造通用型显式时间积分算法求解微分代数方程组,适合于开展大规模并行计算,以达到实时性的目标。
技术指标:
(1)计算效率:单线程计算时,显式积分器的计算效率不低于广义alpha方法
(2)并行计算:云平台上并行线程数或流处理核心数大于10000时仍然能达到线性度的效率提升
(3)集成需求:该技术选题作为实时仿真软件模块,可集成在主流的CAE仿真平台中
技术挑战
1、当前刚柔耦合动力学系统实时仿真存在的问题:
(1). 刚柔耦合动力学系统自由度高、计算复杂度高,只有通过大规模并行才可能达到实时性能;
(2). 隐式积分器需要迭代求解非线性方程组,其计算量不可控,并限制了并行求解度的上限;
(3). 通用的降阶方法导致系统方程组的刚性问题仍然严重,进而显式求解器的时间步长非常小;
(4). 云平台上计算资源分配的特点要求算法能够根据资源量自适应地微调算法以达到实时性。
2、期望实现的技术:
(1). 微分代数方程组的高性能并行显式积分器技术;
(2). 刚柔耦合动力学系统建模中的保稀疏特性降刚性技术。
参考文献
1. Avello, A., Jimenez, J.M., Bayo, E., Dejalon, J.G., 1993. A Simple and Highly Parallelizable Method for Real-Time Dynamic Simulation-Based on Velocity Transformations. Computer Methods in Applied Mechanics and Engineering 107 (3), 313-339.
2. Bae, D.S., Hwang, R.S., Haug, E.J., 1991. A Recursive Formulation for Real-Time Dynamic Simulation of Mechanical Systems. Journal of Mechanical Design 113 (2), 158-166.
3. Bae, D.S., Lee, J.K., Cho, H.J., Yae, H., 2000. An explicit integration method for realtime simulation of multibody vehicle models. Computer Methods in Applied Mechanics and Engineering 187 (1-2), 337-350.
4. Chung, S., Haug, E.J., 1993. Real-Time Simulation of Multibody Dynamics on Shared-Memory Multiprocessors. Journal of Dynamic Systems Measurement and Control-Transactions of the Asme 115 (4), 627-637.
5. Han, S., Choi, H.-S., Choi, J., Choi, J.H., Kim, J.-G., 2021. A DNN-based data-driven modeling employing coarse sample data for real-time flexible multibody dynamics simulations. Computer Methods in Applied Mechanics and Engineering 373.
6. Lee, W.S., Tak, T.O., 1991. Parallel Processing of Controlled Multibody Mechanical System Dynamics. Engineering with Computers 7 (3), 161-172.
7. Pan, Y., Dai, W., Xiong, Y., Xiang, S., Mikkola, A., 2020. Tree-topology-oriented modeling for the real-time simulation of sedan vehicle dynamics using independent coordinates and the rodremoval technique. Mechanism and Machine Theory 143.
8. Pastorino, R., Cosco, F., Naets, F., Desmet, W., Cuadrado, J., 2016. Hard real-time multibody simulations using ARM-based embedded systems. Multibody System Dynamics 37 (1), 127-143.
9. Rodríguez, A.J., Pastorino, R., Carro-Lagoa, Á., Janssens, K., Naya, M.Á., 2020. Hardware acceleration of multibody simulations for real-time embedded applications. Multibody System Dynamics 51 (4), 455-473.
10.Rulka, W., Pankiewicz, E., 2005. MBS approach to generate equations of motions for HiL-simulations in vehicle dynamics. Multibody System Dynamics 14 (3-4), 367-386.
链接:http://www.pi-lab.ac.cn/xsjl/faq/202401/t20240103_202025.html
难题四:AI湍流计算
技术背景
传统湍流模型发展悠久,广泛应用于各行各业。当前工程实践中仍以雷诺平均模型RANS为主,但是在复杂问题上,如汽车外气动,燃料掺混,噪声等问题上,时间尺度瞬态效应明显,RANS模型难以为继,由此使用高保真度湍流模型需求在工业界变得越来越高。直接数值模拟DNS方法要求的空间网格和计算时间步数至少要达到O(Re L 9/4 ) 和O(Re L 1/2 )。当前的计算机能力仍然无法满足。大涡模拟使用滤波函数将瞬时流动分解为大于过滤尺度的大尺度运动和小于过滤尺度的小尺度脉动,引入亚格子模型计算应力对大涡进行能量耗散。
技术挑战
1. 虽然大涡模拟相比于DNS降低了数个量级的计算,但网格数仍比RANS大很多;
2. 较小的网格也会需要小的时间步长来计算,因此需要更多的时间步的迭代才能达到所需的物理计算时长;
3. 不同的网格下选取不同的亚格子模型也需要工程师的经验。
技术诉求
针对汽车风阻仿真场景,利用基于试验数据同化的LES湍流模型进行三维仿真模拟,以仿真数据作为标准训练数据;采用AI建模的方式,训练出一个AI亚格子湍流模型;使其在三维汽车风阻的LES模型仿真场景中,精度与效率得到显著提高。(此技术最终需在国产AI芯片+AI框架+流体力学仿真软件中实现)AI湍流模型的技术指标如下(千万量级网格的三维汽车风阻仿真模拟):
精度:以试验数据为参考,与传统湍流模型相比,气动阻力误差降低30%;
效率:与传统LES湍流模型相比,模拟效率提高4倍以上;
泛化性:在轿车与SUV车型(两种以上的典型车型)、速度(80~150km/h)下同时满足精度与效率指标。
参考文献
链接:http://www.pi-lab.ac.cn/xsjl/faq/202401/t20240103_202029.html
难题五:AI技术提升六面体网格生成自动化问题
技术背景
1. 业务场景:在使用工业软件对各物理场问题分析过程中,相对于其他网格,六面体网格具有更好的计算精度、更高的计算效率、更强的抗畸变能力并能更自然地顺应边界和物理场的走向。目前,六面体网格主要依赖半自动半手工模式--扫掠法来得到。
2. 技术选题的关键性:六面体剖分以扫掠法为主,对一些复杂的工程问题,所需工作量要以人月甚至人年记。如能提升六面体网格生成自动化程度,将大幅减轻工程师的劳动强度,显著提升工作效率,缩短仿真时间和产品开发周期。
3. 技术选题的泛用性:六面体网格生成技术是工业软件和一些相关领域的通用技术,并不局限于某个特定的应用场景。
技术挑战
1. 设计基于AI的三维几何体分块算法,将物体分割为一些适合于扫掠的块。
2. 对于分割后剩余的不可扫掠块,设计AI指导下的空腔填充算法,以填充剩余块内部。
3. 空腔填充算法也应适用于四面体网格。
技术诉求
1. 可自动剖分模型的复杂程度:用基本体素进行10次以内布尔运算得出的几何模型(占比30%)。
2. 对更复杂模型可减少交互工作量30%以上。
3. 单元质量要求:雅可比值不低于0.1。
参考文献
[1] Pietroni N, Campen M, Sheffer A, et al. Hex-mesh generation and processing: a survey[J]. ACM TOG , 2022,42(2): 1-44.
[2] Fang X, Xu W, Bao H, and Huang J. All-Hex Meshing using Closed-Form Induced Polycube. ACM TOG , 2016; 35(4).
[3] Tautges TJ, Blacker T, Mitchell SA. The whisker weaving algorithm: A connectivity-based method for constructing all-hexahedral finite element meshes. IJNME, 1996; 39(19): 3327–3349.
[4] Price MA, Armstrong CG. Hexahedral mesh generation by medial surface subdivision: part II. Solids with flat and concave edges. IJNME, 1997; 40: 111-136.
[5] Livesu M, Pietroni N, Puppo E, Sheffer A, and Cignoni P. LoopyCuts: practical feature-preserving block decomposition for strongly hexdominant meshing. ACM TOG(SIGGRAPH) ; 2020: 39(4).
[6] Lu Y, Gadh R, Tautges TJ. Feature based hex meshing methodology: feature recognition and volume decomposition. Computer Aided Design, 2001; 33(3): 221–32.
[7] Lei, Na , et al. "Quadrilateral mesh generation II: Meromorphic quartic differentials and Abel-Jacobi condition." Computer Methods in Applied Mechanics and Engineering , 2020.
[8] Liu JF, Sun SL, Chen YQ. A new method of quality improvement for quadrilateral mesh based on small polygon reconnection, Acta Mechanica Sinica , 2012, 28(1):140-145.
[9] Biesbroeck A V , Shang F , Bassir D . CAD Model Segmentation Via Deep Learning[J]. International Journal of Computational Methods, 2020.
链接:http://www.pi-lab.ac.cn/xsjl/faq/202401/t20240103_202033.html
如有任何疑问或有合作意向,欢迎联系:吴瑾 lion.wujin@huawei.com


