RSA算法作为现代密码学的重要基石,自1977年诞生以来,一直备受关注。本文将从RSA算法的源代码入手,解析其核心原理,探讨其在实际应用中的价值。
一、RSA算法简介
RSA算法是一种非对称加密算法,由美国麻省理工学院的Rivest、Shamir和Adleman三位学者在1977年发明。RSA算法的安全性建立在数学难题“大数分解”的基础上,至今未被破解。本文将深入解析RSA算法的源代码,以揭示其神秘面纱。
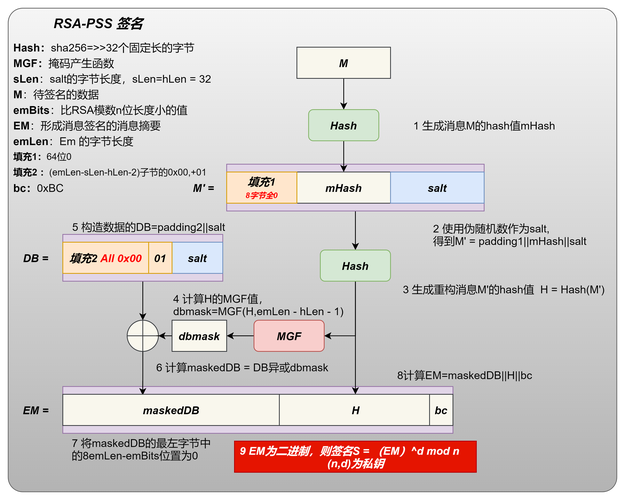
二、RSA算法源代码解析
1. 密钥生成
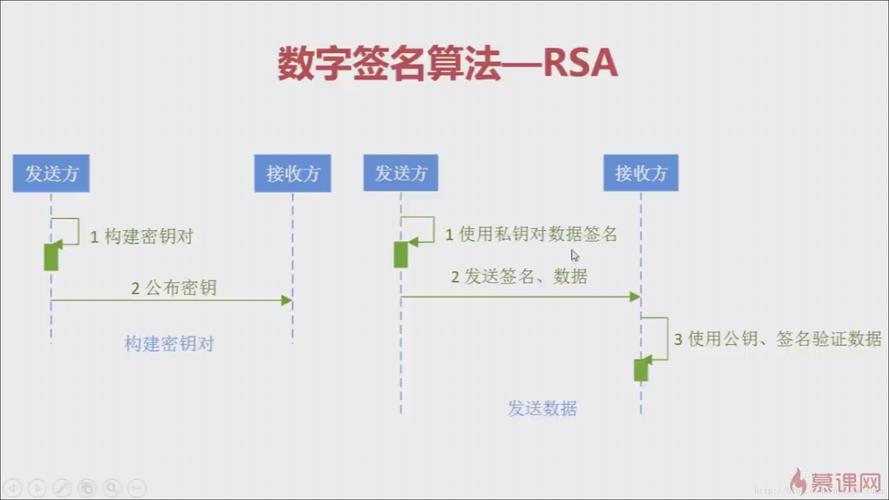
RSA算法的密钥生成主要包括以下几个步骤:
(1)选择两个大质数p和q,它们的长度均为512位。
(2)计算n=pq。
(3)计算欧拉函数φ(n)=(p-1)(q-1)。
(4)选择一个整数e,满足1 (5)计算e关于φ(n)的模逆元d,满足ed≡1(mod φ(n))。 (6)公钥为(e,n),私钥为(d,n)。 2. 加密与解密 (1)加密:将明文M进行模n运算,得到密文C=M^e mod n。 (2)解密:将密文C进行模n的d次幂运算,得到明文M=C^d mod n。 三、RSA算法的实际应用 RSA算法在实际应用中具有广泛的应用场景,如: 1. 数字签名:利用RSA算法对信息进行签名,确保信息的完整性和真实性。 2. 密钥交换:通过RSA算法实现通信双方安全地交换密钥。 3. 数据加密:对敏感数据进行加密,防止数据泄露。 RSA算法作为现代密码学的重要基石,其安全性得到了广泛认可。本文通过对RSA算法源代码的解析,揭示了其核心原理,为读者深入理解RSA算法提供了参考。在未来的发展中,RSA算法将继续发挥其重要作用,为信息安全保驾护航。 参考文献: [1] Rivest, R. L., Shamir, A., & Adleman, L. (1978). A method for obtaining digital signatures and public-key cryptosystems. Communications of the ACM, 21(2), 120-126. [2] Menezes, A. J., van Oorschot, P. C., & Vanstone, S. A. (1997). Handbook of applied cryptography. CRC press.