本文内容:
图遍历算法的简单介绍如何在 Python 上实现它们不同方法的优缺点图遍历算法图遍历算法被认为是最基本但最基本的图算法之一。在设计图算法时,你很可能会引入一些图遍历算法。这个想法是,从顶点 s 开始,你想知道如何到达另一个节点 t:确定从一个节点到另一个节点的路径:图遍历对于查找两个节点是否连接以及是否存在最短路径等很有用
广度优先搜索(BFS)
BFS是一种基本的图遍历算法,由 Edward F. Moore 于 1959 年首次提出,用于寻找走出迷宫的最短路径。BFS 还用于不同的算法,例如最短路径、连通分量搜索和接近中心度计算。
这个想法是,当我们从源节点开始时,我们首先探索其所有直接邻居(一跳距离),然后再移动到其他节点(两跳距离)。这个概念被称为同质性(借用社会学:人们通常与相似的人密切互动),因此相似的节点具有密切的关系。
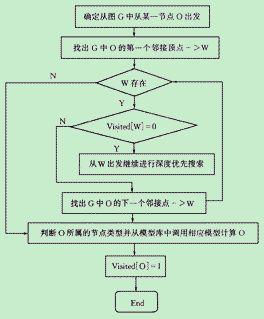
在 BFS 中,我们从节点 s(源)开始,然后开始探索邻居。在一个简单的图中,我们从一个节点开始(图中节点的顺序是任意的),我们将其添加到已访问节点列表中,我们将访问的下一个节点将添加到队列(存储下一个已访问节点的列表)。在下面的段落中,我们访问队列的第一个节点(即 2),从队列中删除节点 2,然后添加它的邻居。这个过程是相同的,直到我们完成队列内的节点。
图片由作者提供
计算时间为 O(n+m),其中 n 是节点数,m 是边数。该算法以线性时间运行,是一种非常高效的算法。通常,这种使用邻接表的算法比邻接矩阵的计算效率更高。访问节点的顺序通常是邻接表顺序。
深度优先搜索(DFS)
这种算法也是由数学家 Charles Pierre Trémaux 发明的,用于解决迷宫问题(很多数学家在迷宫中迷路了,这很有趣)。
从源节点开始,我们移动到直接邻居(我们选择一个),然后我们继续遍历所有路径,然后再回溯。与同质方法相比,这种方法可以更广泛地了解网络中的节点。我们正在寻找节点的结构角色。相似的节点具有所谓的结构等价性。
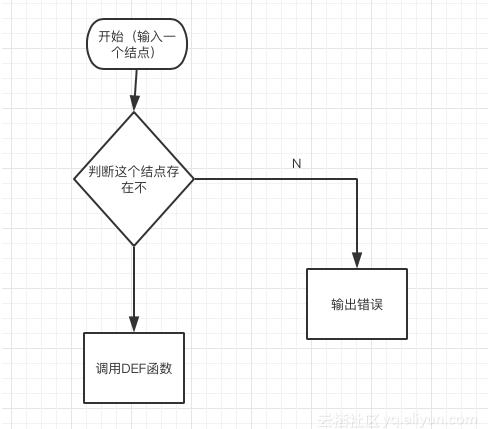
这里我们也从节点 s 开始,访问节点 s 的第一个邻居,然后跳到邻居的邻居。我们的想法是尽量远离起始顶点。这里我将其定义为已访问的节点列表,队列表示我们将要访问的下一个节点。DFS使用堆栈作为结构来存储将要访问的节点(这只是下一个将要访问的节点)。请注意,我们从 1 开始,访问节点 2,而不是访问节点 3,而是访问节点 4。如您所见,我们一直执行此过程,直到有一个节点没有未访问的邻居(如节点 6)。在这种情况下,我们回溯到上一个顶点。
注意,6 只有一个邻居,即 5(但我们已经访问过),因此我们回溯到之前访问过的 6 节点(也是 5)。由于 5 有邻居 4 和 3,我们访问 3,因为 4 已经被访问过。
图片由作者提供
实现方式与 BFS 类似,计算时间为 O(n+m)。请注意,DFS 仅适用于连通图,从源节点无法到达的节点将不会列出(尽管存在针对断开连接的图的修改版本)。
BFS 和 DFS 的应用
BFS 用于查找最小生成树、寻路、在图中搜索循环、点对点网络(如 torrent)、搜索引擎中的爬虫、社交网络网站、GPS 导航系统以及许多其他很酷的应用程序。
BFS 用于社交网络,因为它会先探索邻居,然后再探索邻居的邻居,因此如果我们从一个人开始,我们可能正在寻找的是朋友或朋友的朋友。另一个例子是,在 Facebook 上,你想首先建议朋友的朋友作为新的潜在联系人,而不是网络中远处的人。
DFS 算法用于查找顶点之间的路径、检查图中的循环、测试图是否为二分图、拓扑排序以及解决迷宫和其他谜题。DFS 用于游戏内和谜题解决方案,因为当我们做出决定时,我们会探索从此决定开始的所有路径(如果此决定导致获胜,我们会停止)。在国际象棋或井字棋等游戏中,我们可以将我们的举动想象为对手的举动、我们的回应等等。只有一些举动路径会导致获胜,我们希望找到其中一条通往成功结论的路径。
根据经验法则,您需要使用 BFS 来查找最短路径,测试图是否为二分图,或者找到所有连通分量。DFA 用于决策树并搜索整个图空间。此外,BFS 更适用于稀疏图,而 DFS 更适用于密集图。
在图嵌入中,不同的技术试图在 BFS 和 DFS 之间找到平衡,以探索邻域或网络的发现:BFS 算法强调同质性,而 DFS 强调结构等价性作为在嵌入中捕获的相似性类型(但这是另一个教程的故事)。
Python 实现我将展示如何使用Networkx实现上面绘制的图的算法。让我们设计并绘制一个图 G:
#code to implement with networkximport networkx as nxgraph = { '1' : ['2','3'], '2' : [ '4', '3'], '3' : [ '7', '8'], '4' : ['5', '3'], '5' : ['6'], '6' : [], '7' : [ '8'], '8' : []}G = nx.Graph(graph)nx.draw(G , with_labels= True)
实现 BFS 非常简单:
source = "1"path = nx.bfs_edges(G, source)visited = [source] + [v for u, v in path]visited
['1','2','3','4','7','8','5','6']
DFS 也一样:
source = "1"path = nx.dfs_edges(G, source)visited = [source] + [v for u, v in path]visited
['1','2','4','5','6','3','7','8']
请注意,DFS 比 BFS 更快(每次执行的执行时间可能会有所不同):
import timestart_time = time.time()path = nx.bfs_edges(G, source)print("--- Time execution BFS: %s seconds ---" % (time.time() - start_time))start_time = time.time()path = nx.dfs_edges(G, source)print("--- Time execution DFS: %s seconds ---" % (time.time() - start_time))
iGraph 速度较慢,因此如果需要处理更大的图,请使用 NetworkX:
总之DFS 和 BFS 是由迷失在迷宫中的数学家创建的BFS 首先探索源节点的邻居,而 DFS 则试图远离源节点,深入探索网络它们都可以在线性时间内实现:对于图 G(V, E) 将是 O(V+E)当目标顶点(或解决方案)靠近源节点时,BFS 更合适,相反,如果解决方案远离源,则 DFS 更合适。DFS 比 BFS 更快,而且 DFS 的内存消耗也比 BFS 好结论这些算法构成了许多应用程序和复杂机器学习算法的基础。未来,我们将看到这些算法如何影响诸如 node2vec 或 NN 图本身等应用程序。
参考:https://ai.gopubby.com/graph-ml-graph-traversal-algorithms-in-a-nutshell-a80288a4d604




