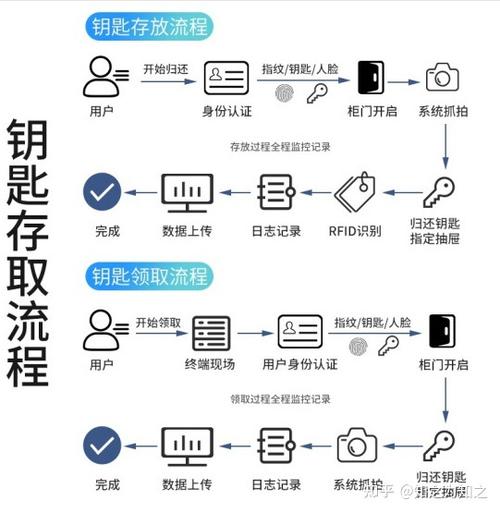
随着科技的不断发展,信号处理技术在我国各行各业中扮演着越来越重要的角色。在众多信号处理算法中,快速傅里叶变换(Fast Fourier Transform,简称FFT)因其高效、稳定的特性而被广泛应用于各个领域。本文将详细介绍FFT算法的原理、实现方法以及在信号处理领域的应用。
一、FFT算法的原理
1. 傅里叶变换

傅里叶变换是信号处理领域的重要工具,它可以将时域信号转换到频域进行分析。傅里叶变换的基本原理是将一个信号分解成不同频率的正弦波和余弦波的叠加。
2. 快速傅里叶变换

由于直接计算傅里叶变换的计算量较大,FFT算法应运而生。FFT算法通过分治策略,将信号分解成较小的部分,从而减少计算量。FFT算法主要包括蝶形运算和分块运算两部分。
(1)蝶形运算:将信号分解成两个部分,分别计算它们的傅里叶变换,然后根据系数进行加权求和。
(2)分块运算:将信号分解成多个子信号,分别计算它们的傅里叶变换,最后将结果合并。
二、FFT算法的实现
1. 线性卷积实现
线性卷积是FFT算法的基础。通过线性卷积,可以将两个信号在时域中的卷积转化为频域中的乘法。以下是线性卷积的MATLAB代码实现:
```matlab
function y = conv(x, h)
[n, m] = size(x);
N = n + m - 1;
y = zeros(1, N);
for i = 1:n
for j = 1:m
y(i + j - 1) = y(i + j - 1) + x(i) h(j);
end
end
end
```
2. 快速傅里叶变换实现
基于线性卷积的FFT算法实现如下:
```matlab
function y = fft(x)
n = length(x);
if n == 1
y = x;
return;
end
even = fft(x(1:2:end));
odd = fft(x(2:2:end));
T = [-1^(k+1) cos(2 pi k / n), sin(2 pi k / n)]';
y = even + odd T;
end
```
三、FFT算法在信号处理领域的应用
1. 通信领域
在通信领域,FFT算法被广泛应用于信号调制、解调、滤波等环节。通过FFT算法,可以将调制后的信号进行频谱分析,从而提高通信质量。
2. 语音信号处理
在语音信号处理领域,FFT算法被用于语音信号的频谱分析、噪声消除、特征提取等环节。通过FFT算法,可以有效地提取语音信号的频域特征,从而实现语音识别、语音合成等功能。
3. 图像处理
在图像处理领域,FFT算法被用于图像的频域滤波、边缘检测、图像恢复等环节。通过FFT算法,可以对图像的频域特征进行分析,从而实现图像增强、图像压缩等功能。
FFT算法作为一种高效、稳定的信号处理算法,在各个领域都得到了广泛的应用。随着科技的不断发展,FFT算法将在未来发挥更加重要的作用。